While working on bergamot-translator, one feature I was tasked with implementing was a translation flow using pivoting. This post is an account of the implementation of the pivoting feature - traversing math I’m to date still not certain of, hacking one thing after another together effectively engineering a feature shipped and running in about 300k installations now.
The idea is simple - given a source language \(ss\) translate to a target language \(tt\), through a pivot language \(pp\). Given how history put us in an anglocentric position, there happens to be a lot of parallel-data between English and other languages of the world, than between other pairs. Sentence aligned parallel data aligned drives machine-translation and this consequently meant the existence of a lot of \(ss \rightarrow en\) models and \(en \rightarrow tt\) models. Consequently pivoting through English to obtain \(ss \rightarrow tt\) remains a prevalent strategy in the field of machine-translation. At the time, the Bergamot Project stood in agreement with its model inventory.
The text part of pivoting is straight-forward. However, one critical-piece to keeping a user-facing HTML translation feature functional was obtaining alignments between the source and target properly. Critical, because the HTML translation feature relied on working alignment information to place tags correctly when matching-tokens in source and target moved around. HTML translation feature was ready with vanilla-translation without pivoting and using alignments. For the pivoting case, attention matrices providing alignments for source to pivot and pivot to target was available separately.
Using these to obtain source to target alignments wasn’t straightforward (at least to me, back then). So I’ve decided this warrants a post, albeit a bit late.
Attention
Marian, the library bergamot-translator is built on top of uses an additional loss formulated using attention to additionally learn alignments between source and target tokens. During training, a guided alignment loss is added to the objective that uses alignment information as a training signal. A tool matching tokens in source to tokens in target from raw-corpus like fastalign can provide alignments that can be used as ground-truths. At inference, the attention values will predict the expected alignments. Note that this is different from learning to align, the network is forced to learn to align to certain ground truths from alignment data here. More on this process can be found in Chen et al. (2016).
Illustrations visualizing attention are often attached as qualitative samples demonstrating attention’s efficacy. The render below comes from something I repurposed with borrowed source from distill.pub.
Translating German to English: Alignments via attention
The above illustration also provide hints to underlying data, and data-structures. The initiated should immediately recognize the tokens (on source and target) can be modelled as nodes and the arrows modelled as weighted edges between source and target tokens.
In code, we have an adjacency-matrix describing the probabilities / scores matching a source-token with a target-token.
Pivoting
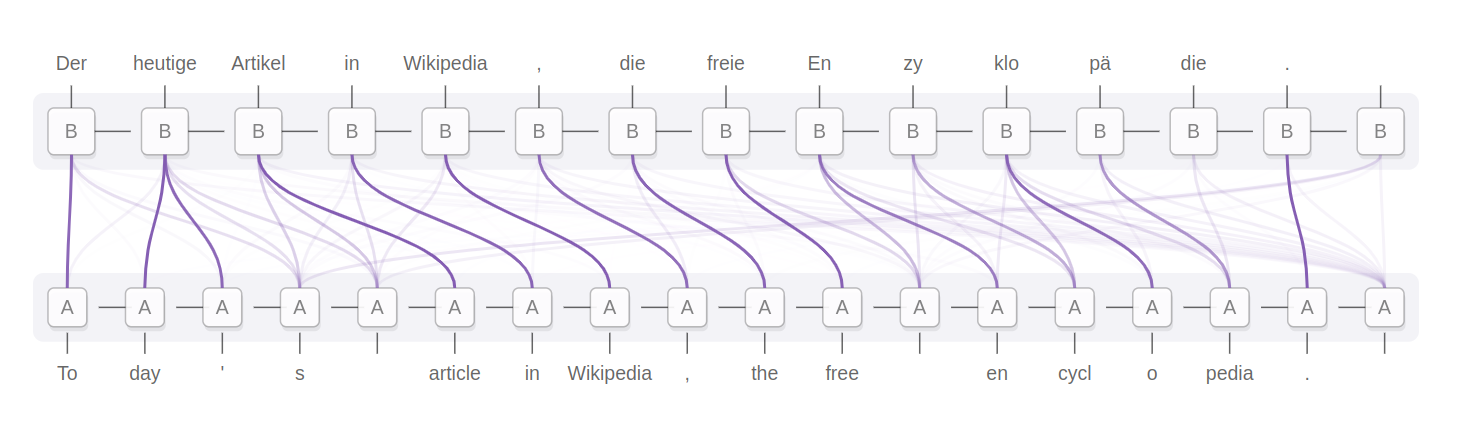
As mentioned before, the idea is simple - given a source language \(ss\) translate to a target language \(tt\), through a pivot language \(pp\). To get a hang of the elements involved in a translation from German to Italian via English as pivot, see illustrations below.

German to English
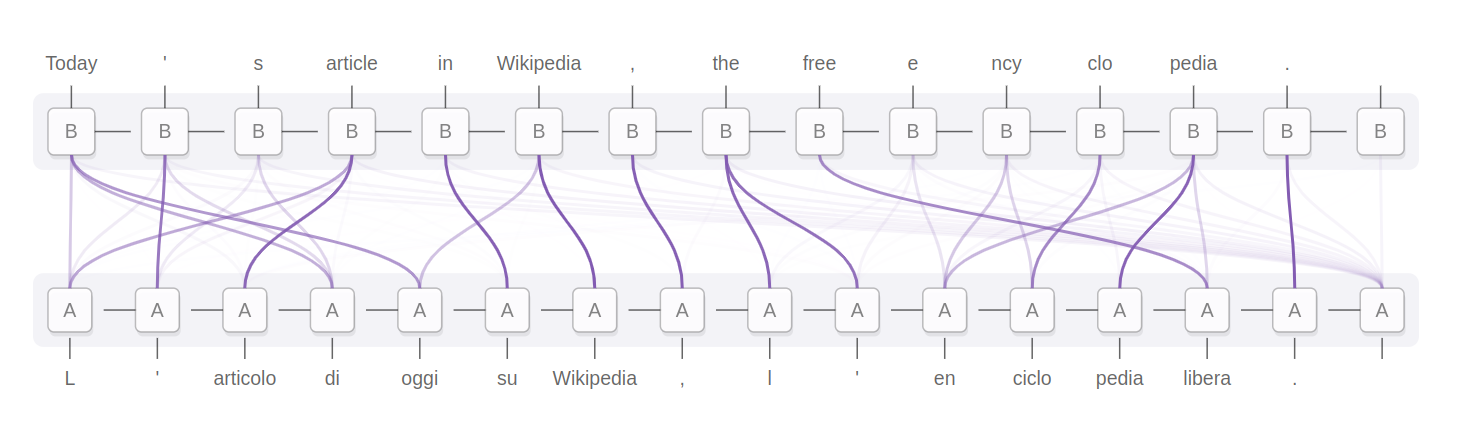
English to Italian
We have two adjacency matrices in-play here, one with scores for source-pivot pair and the other with scores for pivot-target pair. For simplicity’s sake, we’ll first try to come up with a formulation and algorithm for the case when the pivot tokens match (i.e same vocabulary) and matrix multiplication is straighforward.
Same vocabulary
Let the tokens involved in pivoting be \(S, P, T\) denoting source, pivot and target respectively.
\[\begin{align*} S = \{s_i\} &= \{s_1, s_2, \dots \} \\ P = \{q_j\} &= \{q_1, q_2, \dots \} \\ T = \{t_k\} &= \{t_1, t_2, \dots \} \end{align*}\]These tokens do not necessarily correspond to the notion of words. Note that I am using \(q_j\) to represent the pivot sequence \(P\) so as to not confuse with probabilities used in this document, denoted by \(p(\cdot)\).
From alignments coming out of the decoding pipeline, we obtain a probability for each source-token \(s_i\) over the target token \(t_j\). We will use \(p(s_i | t_j)\) to denote this in this post. For each target-token \(t_j\) we have a probability distribution spread over source-tokens \(S\).
We know the values \(p(s_i | q_j)\), \(p(q_j | t_k)\) at inference as some form of attention/alignment from the constituent neural network. I will cook up the math below to get the required \(p(s_i | t_k)\):
\[\begin{align} p(s_i | t_k) &= \sum_{j}{p(s_i, q_j| t_k)} \label{eq:marginalize-pivot} & \text{Marginalization(?)} \\ &= \sum_{j}{{p(s_i| q_j, t_k) \cdot p(q_i | t_k) }} & \text{Bayes rule(?)} \\ p(s_i | t_k) &= \sum_{j}{{p(s_i | q_j)\cdot p(q_j | t_k) }} & \text{Independence(?)} \end{align}\]In an ideal case, if we assume the pivot tokens constituting the pivot sentence are same, we have a \(|S| \times |P|\) matrix and a \(|P| \times |T|\) matrix. The above formulation in implementation translates to a matrix multiplication, of matrices containing attention values coming out of the source to pivot and pivot to target translation processes. Not sure if the above math is sound, I’m mostly working backwards from a gut feeling that I have two attention matrices, multiplying them should give me the required probabilities.
This matrix-multiplication is implemented in bergamot-translator here. The implementation makes an additional hop, due to the vocabularies being different. We will discuss this in detail next.
Different vocabularies
In reality, it’s not as simple as above. Due to historical reasons, the \(ss \rightarrow pp\) and \(pp \rightarrow tt\) models happen to be be using different sets of vocabularies. If we take a closer look at the diagrams above, we see \(P\) and \(P'\) are different. See an extract below. The tokens are space separated.
[S ] Der heutige Artikel in Wikipedia , der freie En zy klo pä die .
[P ] To day ' s article in Wikipedia , the free en cycl o pedia .
[P'] Today ' s article in Wikipedia , the free e ncy clo pedia .
[T ] L ' articolo di oggi su Wikipedia , l ' en ciclo pedia libera .
The previous formulation was convenient in our application of NMT case when the vocabulary used to represent the language \(pp\) is consistent giving us \(S \leftarrow P\) and \(P \leftarrow T\). To obtain the probabilities in the inconsistent case, we can use the knowledge that vocabularies match at character or byte level. Both vocabularies describe the same underlying text-surface.
Updating the formulation to include inconsistent pivot vocabularies, we get:
\[\begin{align*} S = \{s_i \} &= \{s_1, s_2, \dots \} \\ P = \{q_j \} &= \{q_1, q_2, \dots \} \\ P' = \{q'_{j'}\} &= \{q'_1, q'_2, \dots \} \\ T = \{t_k \} &= \{t_1, t_2, \dots \} \\ \end{align*}\]The old math remains valid, but requires some reinterpretation. We will start from the formulation we already have.
\[\begin{align} p(s_i | t_k) &= \sum_{j}{{p(s_i | q_j)\cdot p(q_j | t_k) }} \\ \end{align}\]Both \(q'_{j'}\) and \(q_j\) describe a surface in the same underlying string, which overlaps to some extent. We can use this information to proportionately assign probabilities of \(q'_{j'}\) to the characters, and reinterpret them in terms of \(q_j\).
\[\begin{align*} p(q_j | t_j) &= \sum_{q'_{j'}}{\mathrm{overlap}(q_j, q'_{j'}) \cdot p(q'_{j'} | t_j)} \\ \mathrm{overlap}(q_j, q'_{j'}) &= \dfrac{\lvert q_j \cap q'_{j'} \rvert}{\lvert q'_{j'} \rvert} \\ \end{align*}\]Validation
I have cooked up a lot of math, now how do I validate it? Thankfully this is grounded in a real use-case. I can try and do German to English to Italian, but the weird thing is I don’t speak/read the source and target languages. I came up with the not-so-standard but useful use-case of translating English to Estonian to English doing the round-trip.
The above process is textbook definition of lost in translation. When translating through an intermediate language, some information is lost (or added). Some corruption to the tokens happen. However, should the alignment formulations and engineering be sound the scores should correspond for the tokens surviving lost in translation.
Armed with the above, I filtered out the top-scores and printed them on the console during development. Find some output from the time of development below (click to expand).
Sample #1
> The Bergamot project will add and improve client-side machine translation in a web browser.
< The Bergamot project will add and improve the translation of the client-side machine into a web browser.
The The=0.955146
Berg Berg=0.826679
amo amo=0.995598
t t=0.975599
project project=0.955401
will will=0.912722
add add=0.623312
and and=0.941392
improve improve=0.710752
translation the=0.21632
translation translation=0.636088
- of=0.396329
machine the=0.685785
machine client=0.437611
client -=0.627738
client side=0.621546
machine machine=0.720943
in into=0.888125
a a=0.951628
web web=0.778772
row b=0.541725
ser row=0.273472
ser ser=0.293319
. .=0.925082
will =0.0982262Sample #2
> Unlike current cloud-based options, running directly on users’ machines empowers citizens to preserve their privacy and increases the uptake of language technologies in Europe in various sectors that require confidentiality.
< Unlike current cloud-based options, working directly on user machines allows citizens to preserve their privacy and increases the adoption of language technologies in Europe in various sectors that require confidentiality.
Unlike Unlike=0.695362
options current=0.526343
cloud cloud=0.808333
based -=0.519486
based based=0.494906
options options=0.726565
, ,=0.953748
running working=0.639273
directly directly=0.927166
on on=0.712787
users user=0.304554
machines machines=0.624575
empower allows=0.385191
citizens citizens=0.503892
to to=0.443355
preserve preserve=0.797836
their their=0.776323
privacy privacy=0.942544
and and=0.947178
increases increases=0.786974
the the=0.646595
take adoption=0.835365
of of=0.510325
language language=0.873498
technologies technologies=0.815092
in in=0.853544
Europe Europe=0.7521
in in=0.87099
various various=0.948102
sectors sectors=0.864905
that that=0.706083
require require=0.929663
confidentiality confidentiality=0.754831
. .=0.937042
options =0.068332Sample #3
> Free software integrated with an open-source web browser, such as Mozilla Firefox, will enable bottom-up adoption by non-experts, resulting in cost savings for private and public sector users who would otherwise procure translation or operate monolingually.
< Free software integrated with an open source web browser, such as Mozilla Firefox, will allow the adoption from the bottom up by non-experts, resulting in cost savings for public and private sector users who would otherwise acquire translation or operate monolinguily.
Free Free=0.56728
software software=0.62599
integrated integrated=0.883837
with with=0.947031
an an=0.839987
open open=0.754714
source source=0.690299
web web=0.729925
row b=0.353977
ser row=0.299766
ser ser=0.309285
, ,=0.813261
as such=0.704488
as as=0.557725
Mo Mo=0.860583
z z=0.997161
illa illa=0.978077
Fire Fire=0.983289
fo fo=0.996755
x x=0.99419
, ,=0.851676
enable will=0.72535
enable allow=0.251865
adoption the=0.261452
adoption adoption=0.643473
bottom from=0.282512
bottom the=0.456695
bottom bottom=0.460874
up up=0.47468
by by=0.623741
non non=0.832823
non -=0.305707
expert expert=0.71779
non s=0.252237
, ,=0.891577
resulting resulting=0.386231
in in=0.745363
cost cost=0.685577
savings savings=0.798135
for for=0.787879
private public=0.50413
private and=0.594041
private private=0.719888
users sector=0.415775
users users=0.790084
who who=0.679675
would would=0.659394
otherwise otherwise=0.823563
procure acquire=0.834951
translation translation=0.743358
or or=0.935836
operate operate=0.720217
mono mono=0.744872
ling ling=0.626815
ual u=0.684935
ly ily=0.676535
. .=0.69808j
ly =0.0632002Sample #4
> Bergamot is a consortium coordinated by the University of Edinburgh with partners Charles University in Prague, the University of Sheffield, University of Tartu, and Mozilla.
< Bergamot is a consortium coordinated by the University of Edinburgh with partners from Charles University in Prague, the University of Sheffield, the University of Tartu and Mozilla.
Berg Berg=0.994895
amo amo=0.991532
t t=0.967724
is is=0.888633
a a=0.894048
consortium consortium=0.868016
coordinated coordinated=0.773978
by by=0.935519
the the=0.738964
University University=0.929871
of of=0.946889
Edinburgh Edinburgh=0.936051
with with=0.817898
partners partners=0.867468
Charles from=0.216679
Charles Charles=0.731952
University University=0.624898
in in=0.875768
Prague Prague=0.87894
, ,=0.938541
the the=0.589038
University University=0.910463
of of=0.902571
She She=0.881999
f f=0.992118
field field=0.992631
, ,=0.842823
University the=0.517793
University University=0.835048
of of=0.89574
Tar Tar=0.918662
tu tu=0.947869
and and=0.821724
Mo Mo=0.884175
z z=0.972944
illa illa=0.993525
. .=0.926998
University =0.0469722Turns out, the tokens match most of the time strong when they’re same. The implementation works as intended!
The implementation of the above reinterpretation for vocabulary mismatch is available here. This code in action, through the alignments visualization pipeline I get the following render:
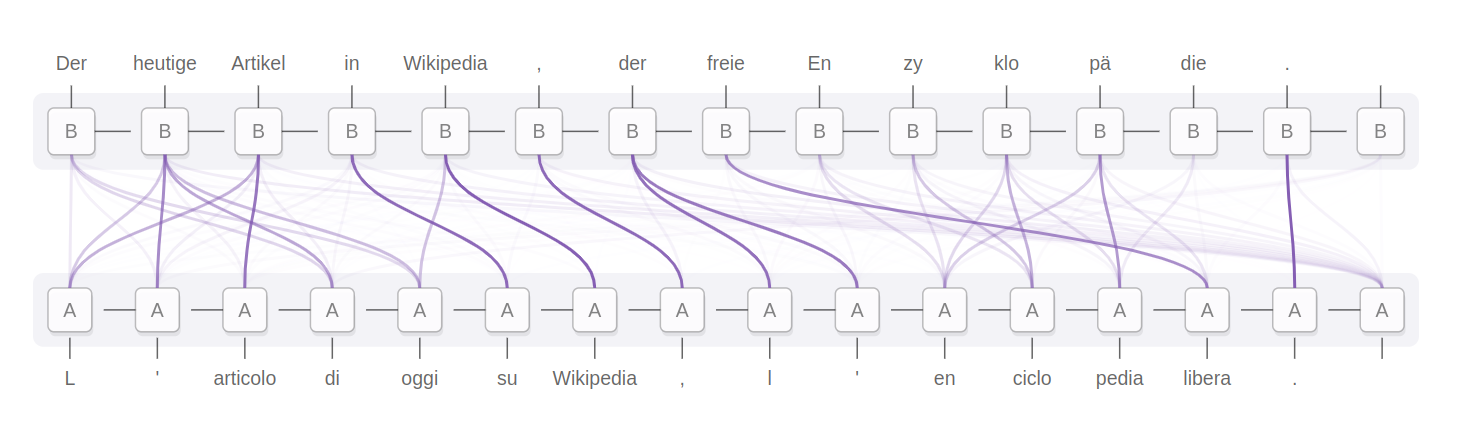
German to Italian: alignments after corrections following pivoting.
Arrows appear to be pointing in the right direction as well. libera corresponds to freie - this is one case where corresponding tokens have moved around to a different position in translation. The force looks strong between the nodes in the cluster forming enciclopedia and Enzyklopädie. Artikel and articolo, Wikipedia and Wikipedia looks strong as well.
The test-in-the wild for this piece of code is transferring links and formatting in inline-text. So if you find yourself using Mozilla Firefox’s offline translation addon and the links and formatting like bold/italic etc transferring from source HTML to target HTML for non-English pairs accurately, this post is an excuse for an explanation why.
References
Wenhu Chen, Evgeny Matusov, Shahram Khadivi, and Jan-Thorsten Peter. 2016. Guided alignment training for topic-aware neural machine translation. arXiv preprint arXiv:1607.01628.